Sketch some level curves of the function Solution First, let z be equal to k, to get f(x,y) = k Secondly, we get the level curves, or Notice that for k>0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves ofDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane
Level Curves Geogebra Dynamic Worksheet
Level curves calculator
Level curves calculator-Level Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andLEVEL CURVES Example 11 Then compare the formed surface with the graph of g a from MATH MISC at University Of Arizona



Level Curves Of The Error After Iterations The Star Marks The Download Scientific Diagram
The level curves in this case are just going to be lines So, for instance, if we take the level curve at z equals 0, then we have just the equation 2x plus y equals 0 And so that has intercept so we're looking at so 0 equals 2x plus y, so that's just y equals minus 2x So that's this level curveIf you take a perfectly horizontal sheet or plane that's parallel to the xyplane, and you use that to slice through your threedimensional figure, then what you get at the intersection of the figure and the plane is a twodimensional curve What we want to be able to do is slice through the figure at all different heights in order to get what we call the "level curves" of a functionThe level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy planeLevel curve definition, contour line See more The height of the tower from the level of the street is 105 feet, the slated towers over the lateral pediments being smallerLevel curves Loading level curves level curves Log InorSign Up x 2 y 2 − z 2 = 1 1 z = − 0 8 2 3
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionLet $f(x,y) = x^2y^2$ We will study the level curves $c=x^2y^2$ First, look at the case $c=0$ The level curve equation $x^2y^2=0$ factors to $(xy)(xy)=0$ This equation is satisfied if either $y=x$ or $y=x$ Both these are equations for lines, so the level curve for $c=0$ is two lines2D and 3D isoline plots Label Contour Plot Levels This example shows how to label each contour line with its associated value



Solved Describe The Level Curves Of The Function Z 8 2x Chegg Com
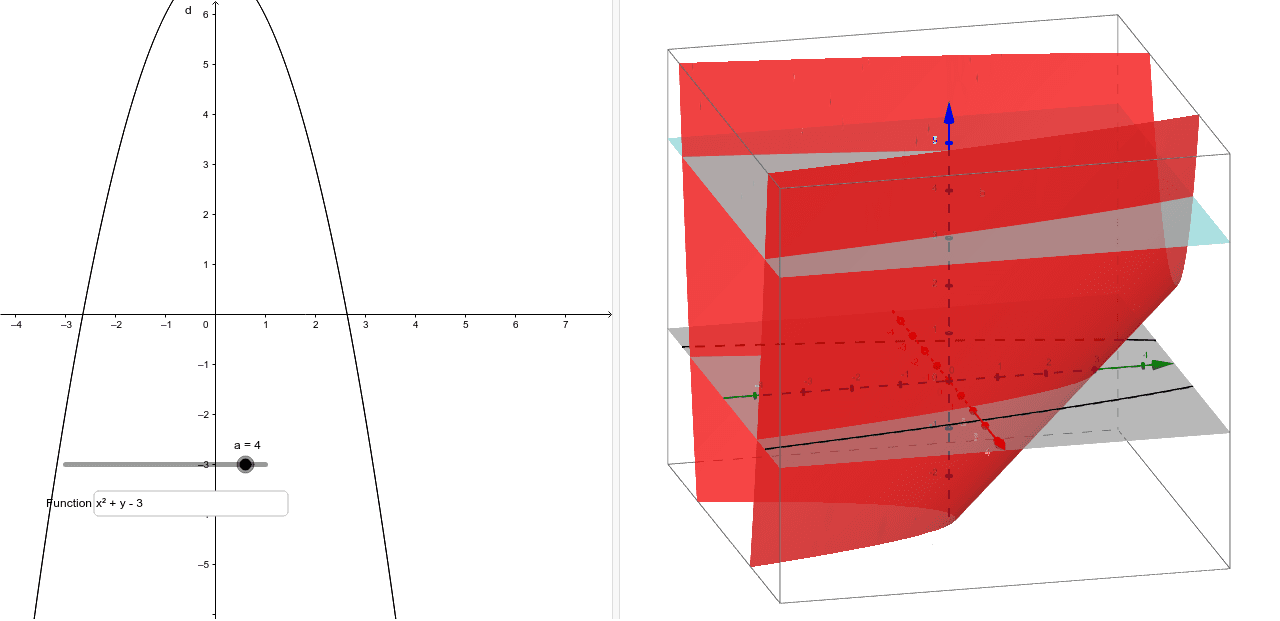


Visualizing Level Curves Geogebra
Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kThe level curve equation x 2 − y 2 = 0 factors to (x − y) (x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If c ≠ 0, then we can rewrite the level curve equation c = x 2 − y 2 asThe level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;



Level Curves Of The Error After Iterations The Star Marks The Download Scientific Diagram
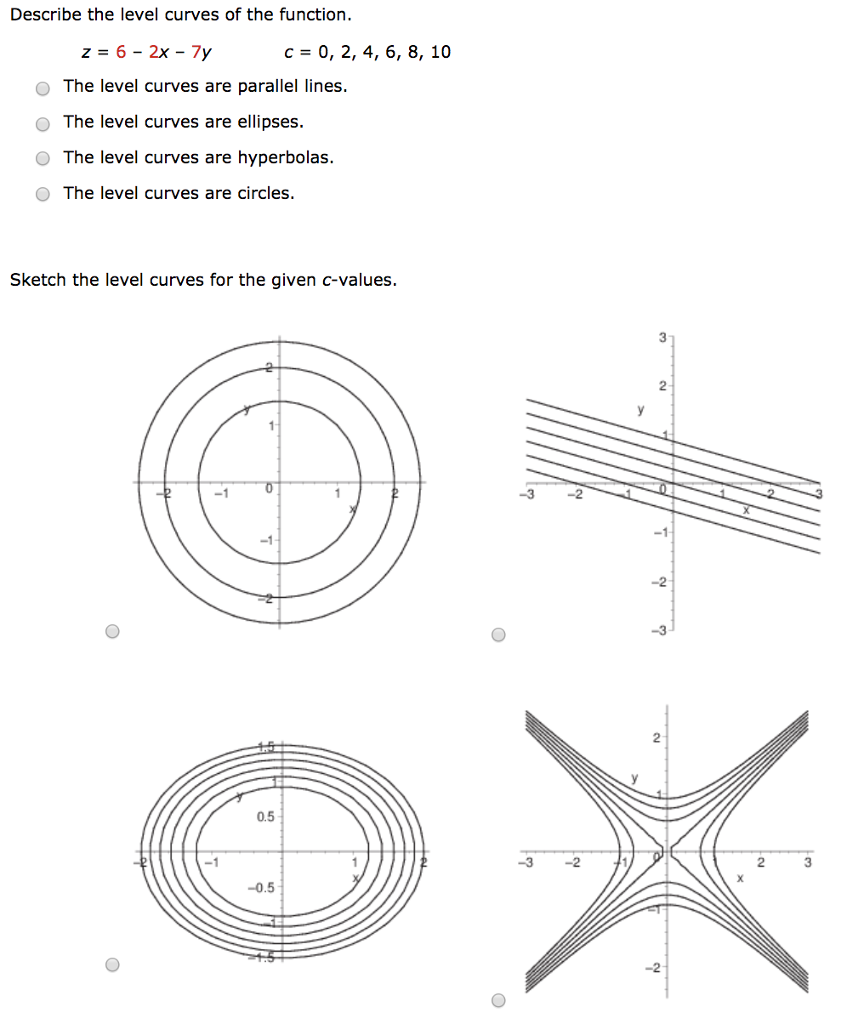


Solved Describe The Level Curves Of The Function Z 6 2x Chegg Com
How to plot level curves of f (x,y) = 2x^2 5y^2 f (x,y) = c for c = 1,2,3,4,5,6 I have never used matlab before and have no idea how to plot level curves I looked online and most results involve using contour but not exactly sure how to specify the upper limit of z Sign in to answer this questionLevel Curves For a general function z = f ( x, y), slicing horizontally is a particularly important idea Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = cLevel Curves Recall that the pole in polar coordinates is the{eq}z {/eq}axis When we expand from two to three dimensions, we essentially enable ourselves to move up and down that pole
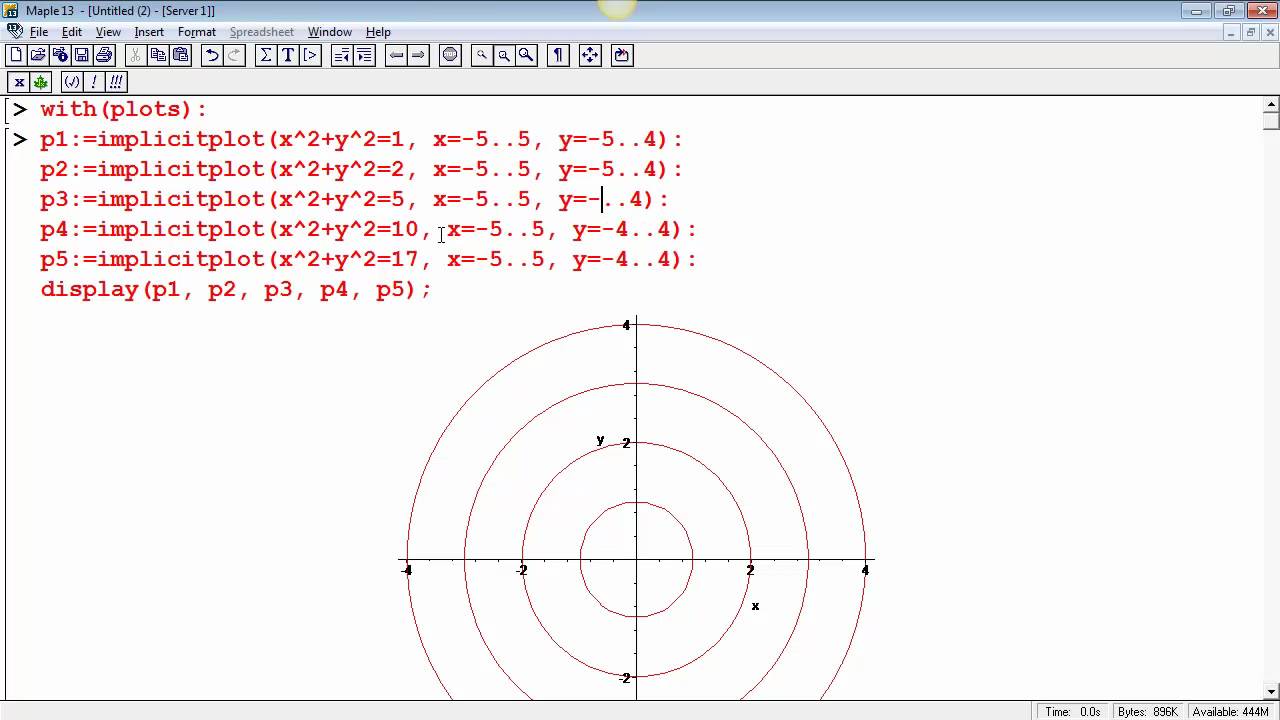


Level Curves Part 2 Cone Hyperboloid Ellipsoid Youtube


Contour Lines Rodolphe Vaillant S Homepage
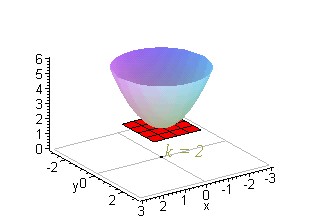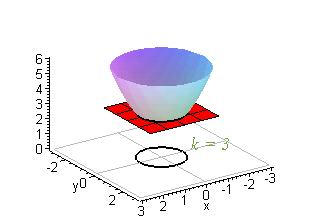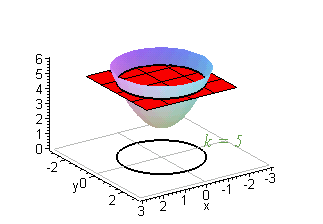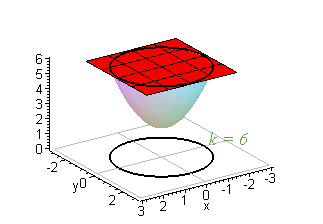
Then the curves obtained by the intersections of the planes $z = k$, $k \in \mathbb{R}$ with the graph of $f$ are called the Level Curves of $f$ From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$ axis and the surface generated by the function $z = f(x, y)$Well, if you think about it, if I fix the value of z, then this is exactly the equation for the circle with radius square root of z So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplaneAccording to the definition of level curves, if we are given a function of two variables z = f (x, y),the crosssection between the surface and a horizontal plane is called a level curve or a contour curve Thus, level curves have algebraic equations of the form f (x, y) = k for all possible values of k



Level Sets Math Insight
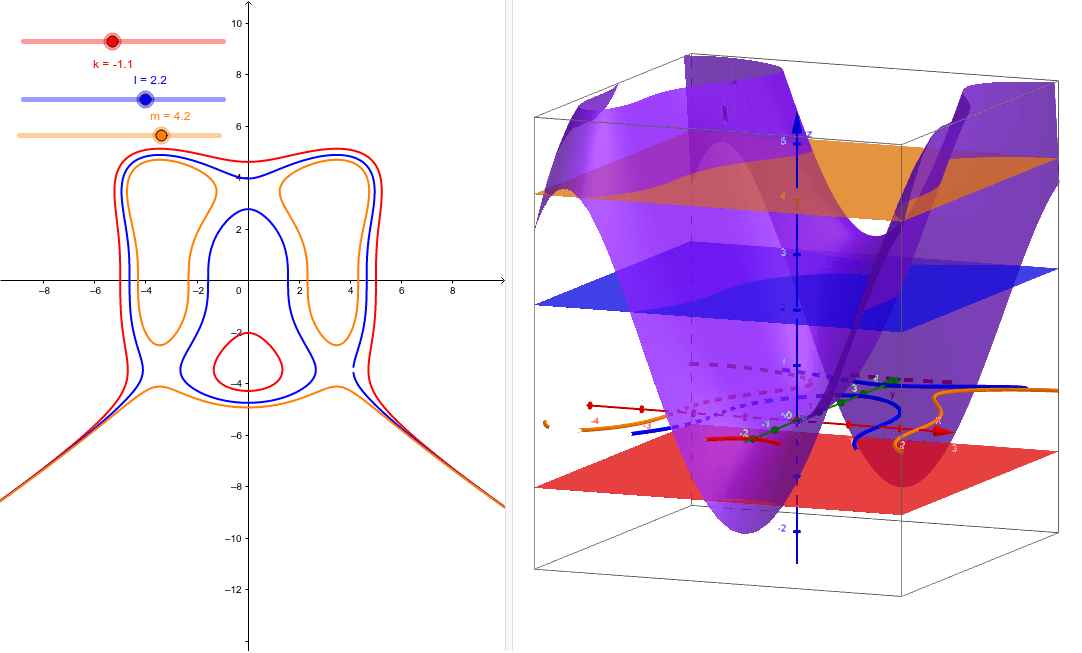


Function Of Several Variables Several Level Curves Geogebra
Section 31 Parametric Equations and Curves To this point (in both Calculus I and Calculus II) we've looked almost exclusively at functions in the form \(y = f\left( x \right)\) or \(x = h\left( y \right)\) and almost all of the formulas that we've developed require that functions be in one of these two formsGet the free "Plotting a single level curve" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaSolution First, let z be equal to k, to get f (x,y) = k Secondly, we get the level curves, or Notice that for k >0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves of f (x,y)



Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F Xy Study Com


Gradients And Level Curves
Level curves Level Curves For a general function $z = f (x,\,y)$, slicing horizontally is a particularly important idea Level curves for a function $z=f (x,\,y) \, D \subseteq {\mathbb R}^2 \to {\mathbb R}$ the level curve of value $c$ is the curve $C$ in $D \subseteq {\mathbb R}^2$ on which $f\Bigl_ {C} = c\, $The level curves of are curves in the plane along which has a constant value For, the level curve of value is given by We now sketch the resulting curves for a couple values of The curve consists of all points satisfyingSolution for Graph several level curves of the following function using the given window Label at least two level curves with their zvalues z= 3x y


Level Curves Geogebra



Level Curves
TestfileMon Feb 22 2143 CET ;The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;Level curves are a way of giving visual information about a surface in R 3 in a 2dimensional form E xample 1 6 1 Let f (x, y) = x 2 y 2 If k > 0, the level curve defined by f (x, y) = k is the circle x 2 y 2 = k If k = 0 then the level curve is the single point {0} and if k < 0, then the level curve does not exist (since the range of



Level Curves



Gradient And Level Curve Geogebra
Question Graph Several Level Curves Of The Following Function Using The Given Window Label At Least Two Level Curves With Their Zvalues 25 Cos (3x y 12,2*221 Choose The Correct Graph Below OD Ос ОА овThe level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;TestfileMon Feb 22 CET


Relief Functions And Level Curves


Level Curves
Level curves themselves can give us information about the rate of increase The more closely spaced they are, the faster the increase, but by themselves, they cannot tell us whether the curve is increasing or decreasing It's the gradient that gives us that So consider the graph below showing the gradient only What can you tell(* Command to plot level curves of f (x, y) = x^2 y^2 *) ContourPlotx^2 y^2, {x, 4, 4}, {y, 4, 4} The default output plots 10 level curves in shaded gray scale, with lighter shades corresponding to larger values of z The following more detailed command plots five level curves without shading Try it!A level curve f ( x, y) = c of a smooth, nowhere constant function, if it is bounded, typically consists of one or more closed curves A sufficient condition for f ( x, y) = c to be bounded is that f ( x, y) → ∞ as x y → ∞ The level curve is a subset of the domain


Level Curves And Contour Plots Mathonline



Describe The Sketch Of The Level Curves Of The Function F X Y 7x 2y For Z 19 9 Study Com
Level curves are a way of giving visual information about a surface in R 3 in a 2dimensional form E xample 1 6 1 Let f (x, y) = x 2 y 2 If k > 0, the level curve defined by f (x, y) = k is the circle x 2 y 2 = k If k = 0 then the level curve is the single point {0} and if k < 0, then the level curve does not exist (since the range ofSo level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming fromA level curve of a function f (x,y) is the curve of points (x,y) where f (x,y) is some constant value, on every point of the curve Different level curves produced for the f (x,y) for different values of c can be put together as a plot, which is called a level curve plot or a contour plot Every contour line in a contour plot is drawn for different value of z, each value a constant



How To Sketch Level Curves Vector Calculus Youtube



Solved Sketch The Level Curves Of The Function G X Y Chegg Com
A level curve of a function f (x,y) is the curve of points (x,y) where f (x,y) is some constant value, on every point of the curve Different level curves produced for the f (x,y) for different values of c can be put together as a plot, which is called a level curve plot or a contour plotA level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14)Colored paper strips for a torus;



Gradients And Level Curves


File Crosshatch 3d Plot With Projected Level Curves Png Wikimedia Commons
New Resources Unit Circle device;Colored paper strips for a torus;Level Curves Recall that level curves are slices through surfaces Essentially each constant z z value is a "level" of the surface, so we can find level curves by seeting z= k z = k, a constant



Drawing Level Curves Of A Minimum Function Mathematics Stack Exchange


Relief Functions And Level Curves
Solution First, let z be equal to k, to get f (x,y) = k Secondly, we get the level curves, or Notice that for k >0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves of f (x,y)Select Level Curves from the Options menu Click the Color Density button Click the OK button Select Plot from the Graph menu Select Level Curves from the Options menu Click the Pattern Density button Click the OK button Select Plot from the Graph menu Example 2 z = f(x, y) = 3y/(x^2y^21) Select Level Curves from the Options menuSection 31 Parametric Equations and Curves To this point (in both Calculus I and Calculus II) we've looked almost exclusively at functions in the form \(y = f\left( x \right)\) or \(x = h\left( y \right)\) and almost all of the formulas that we've developed require that functions be in one of these two forms



Level Curves Geogebra Dynamic Worksheet


Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
TestfileMon Feb 22 2143 CET ;TestfileMon Feb 22 CETLevel Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both and



Level Sets Math Insight



Calculus Iii Functions Of Several Variables
Solution for Graph several level curves of the following function using the given window Label at least two level curves with their zvalues z= 3x yLevel curves Level Curves For a general function $z = f (x,\,y)$, slicing horizontally is a particularly important idea Level curves for a function $z=f (x,\,y) \, D \subseteq {\mathbb R}^2 \to {\mathbb R}$ the level curve of value $c$ is the curve $C$ in $D \subseteq {\mathbb R}^2$ on which $f\Bigl_ {C} = c\, $Level Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both and



Level Curves Of Functions Of Two Variables Youtube
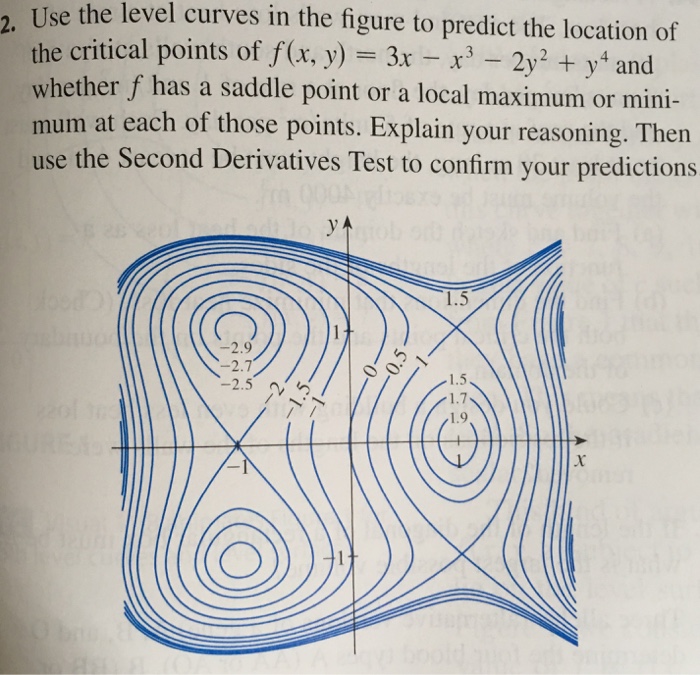


Solved Use The Level Curves In The Figure To Predict The Chegg Com
New Resources Unit Circle device;



How Do You Plot Level Curves Describing A 3d Surface On The X Y Plane Mathematica Stack Exchange



The Figure Shows Level Curves Of A Function F In The Square R 0 6 Times 0 6 Use The Midpoint Rule With M N 2 To Estimate
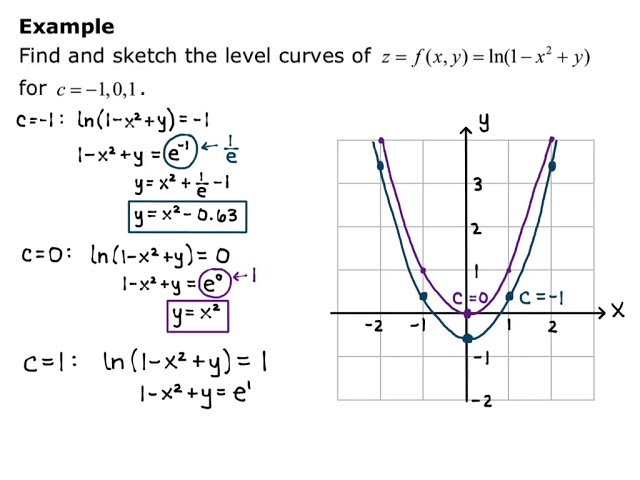


Section 13 1 Level Curves Youtube


Level Curves Geogebra



How To Sketch Level Curves Youtube


Level Curves And Contour Plots Mathonline
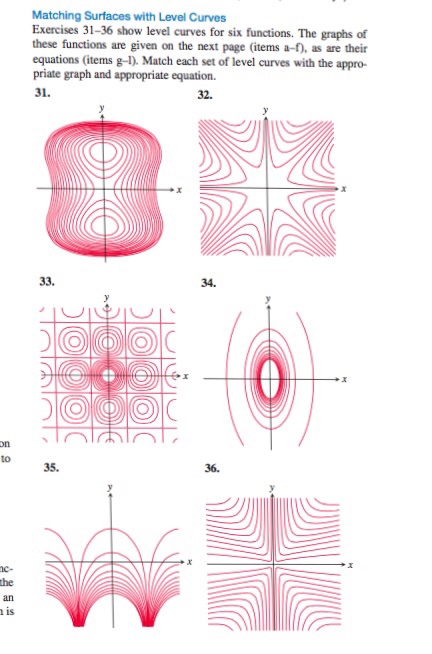


Solved Matching Surfaces With Level Curves Exercises 31 3 Chegg Com



Graph And Level Curves Of The Melnikov Potential L 1 I ϕ S With Download Scientific Diagram


Functions Of Several Variables



Level Set Examples Math Insight
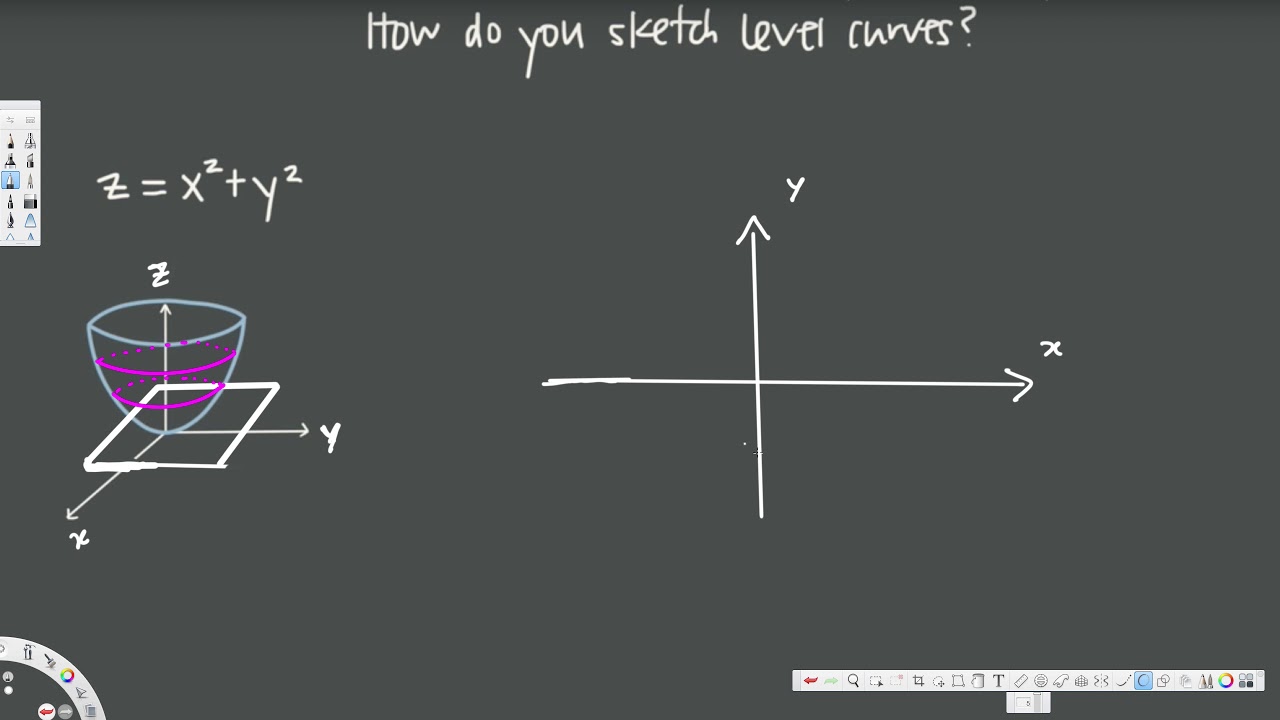


How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube
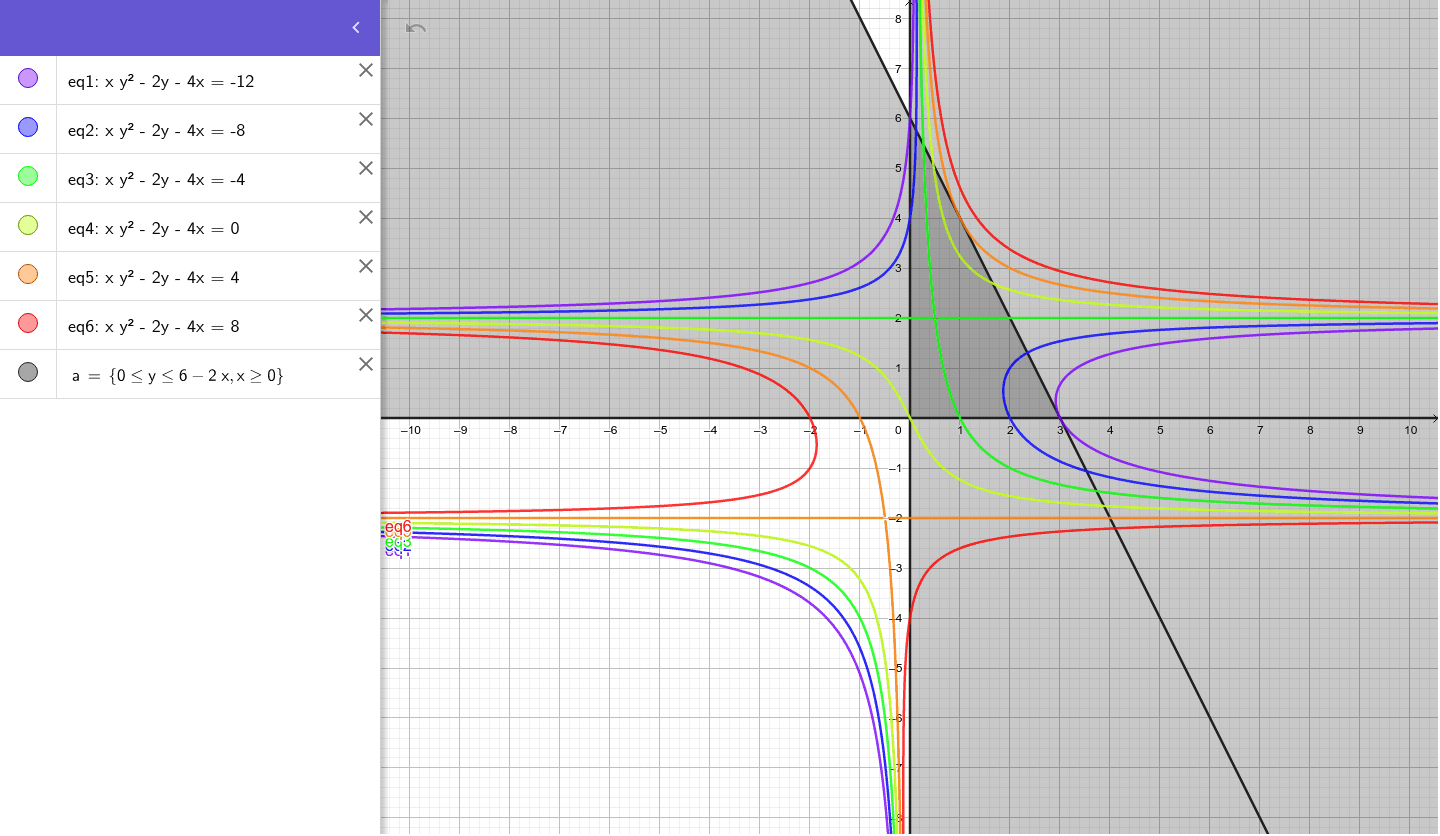


Level Curves Geogebra



Oneclass Sketch The Level Curves Of The Function For K 0 3 4 5 Example 11 Sketch The Level Curves



Use The Level Curves In The Figure To Predict The Location Of The Critical Points Of F And Whether F Has A Saddle Point Or A Local Maximum Or Minimum At Each


0 3 Visualizing Functions Of Several Variables
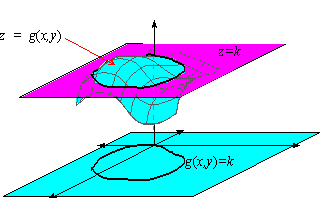


Gradients And Level Curves



Graphs And Level Curves


Functions Of Two Variables Lessons Blendspace
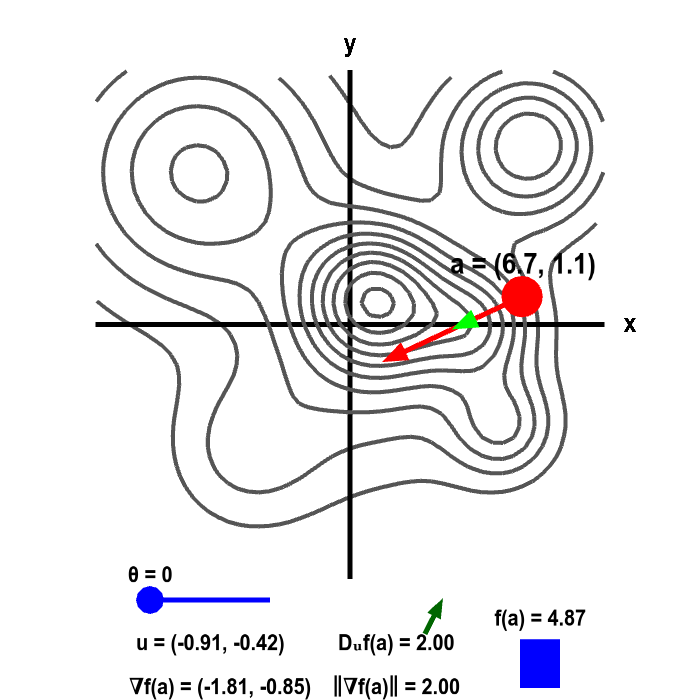


Applet Gradient And Directional Derivative On A Mountain Shown As Level Curves Math Insight


Level Curves And Contour Plots



Negative Level Curves Of X P A X And X P B X Download Scientific Diagram
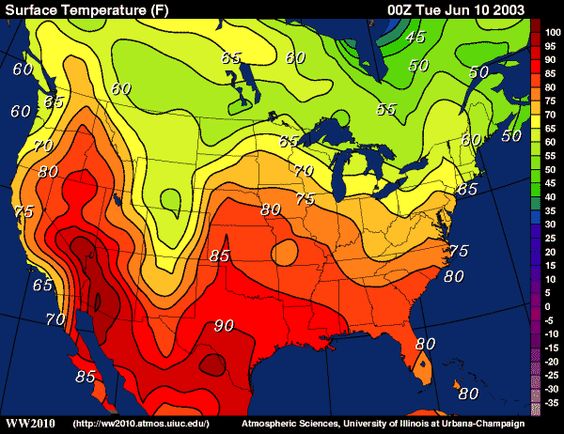


Level Sets Ximera


Sketch The Level Curves For The Following Functions And The Values 2 1 1 2 And Describe Sarthaks Econnect Largest Online Education Community



How To Draw Level Curves For X X 2 Y 2 Mathematics Stack Exchange
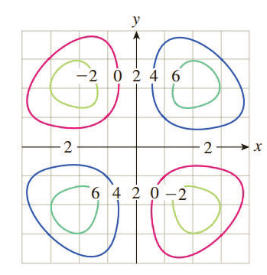


Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4
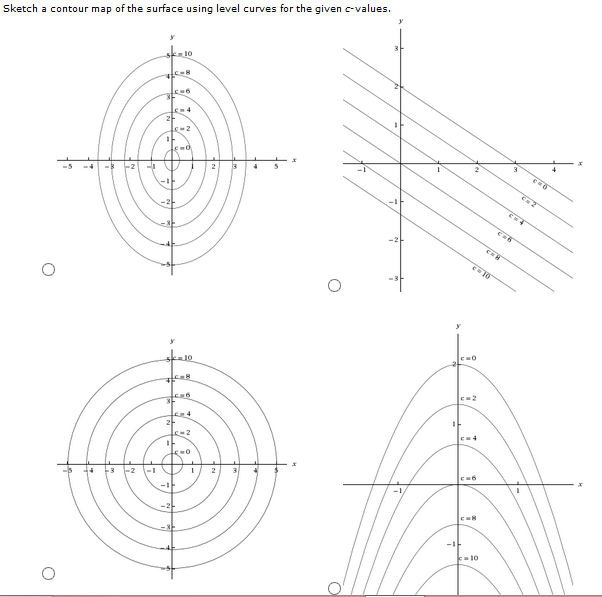


Solved Z 6 2x 3y C 0 2 4 6 8 10 O The Level Curves Chegg Com



Level Sets Ximera



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 3 Youtube



Solutions To Homework 1 1 The Level Curves Are Determined



Applet Level Curves Of A Hyperbolic Paraboloid Math Insight



Solved Describe The Level Curves Of The Function Z X2 Chegg Com



16 1 Functions Of Several Variables



Use The Level Curves In The Figure To Predict The Location Of The Critical Points Of F And Whether F Has A Saddle Point Or A Local Maximum Or Minimum At Each


Functions Of Several Variables Ximera


Level Curves
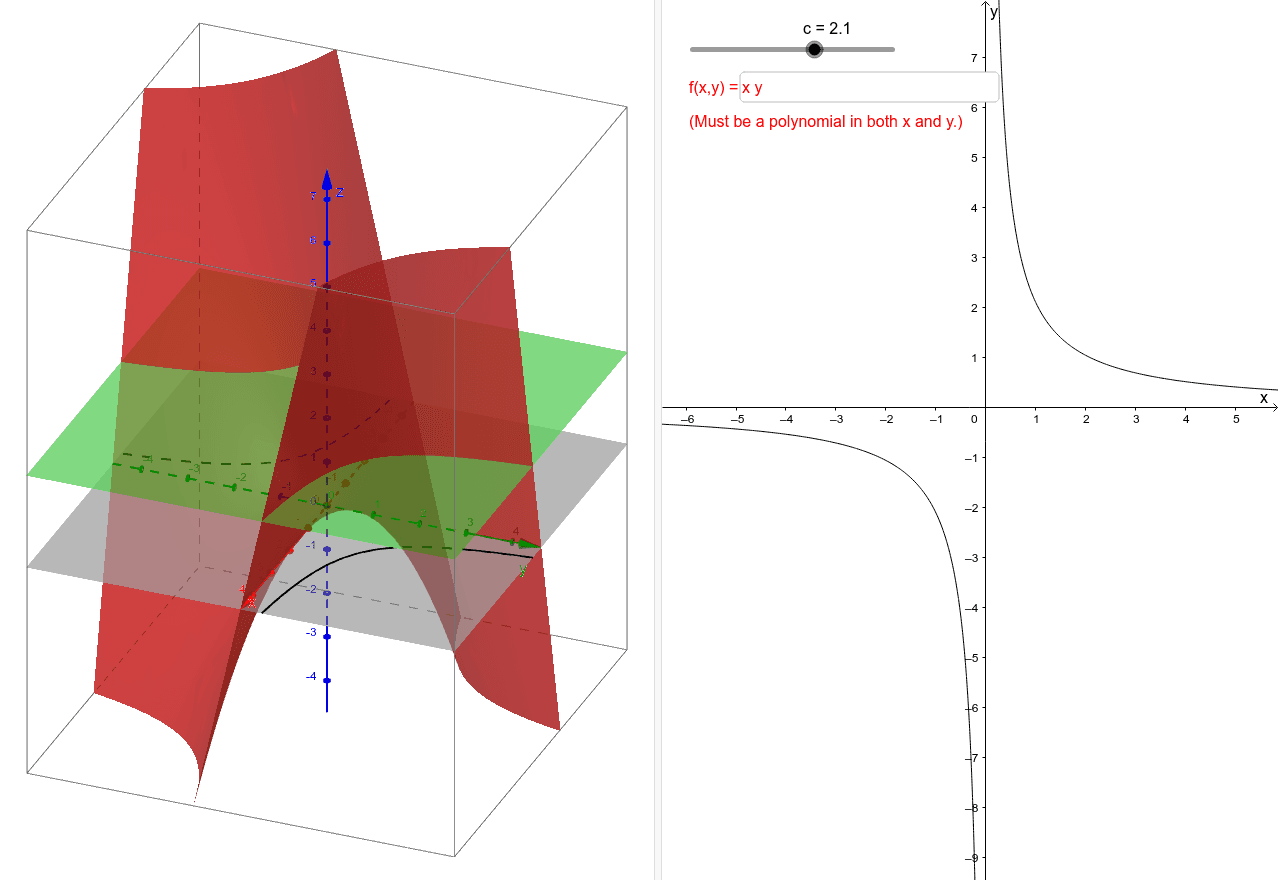


Level Curves Geogebra



Visualizing Surface And Level Curves Youtube



Some Level Curves For The Total Energy E U V The Trajectory That Download Scientific Diagram



The Figure Shows The Level Curves Of The Two Payoff Functions Here Download Scientific Diagram



Level Curves


Draw Level Curves For Functions Of Two Variables In C C Helper


Level Curves Project Project



Level Sets Math Insight



Level Curve And A Surface Tex Latex Stack Exchange



Level Curves Of Function At Z 0 Mathematics Stack Exchange


Problem Of Level Curves Leading Lesson


12 1 Introduction To Multivariable Functions Mathematics Libretexts



Relation Between Level Curves And Horizontal Traces Tex Latex Stack Exchange



Left Level Curves Of Distorted Density F X Y Center Level Download Scientific Diagram



Level Set Wikipedia



Level Curves C 4 R T W C For C 0 3 Dashed Lines And C 0 1 Download Scientific Diagram
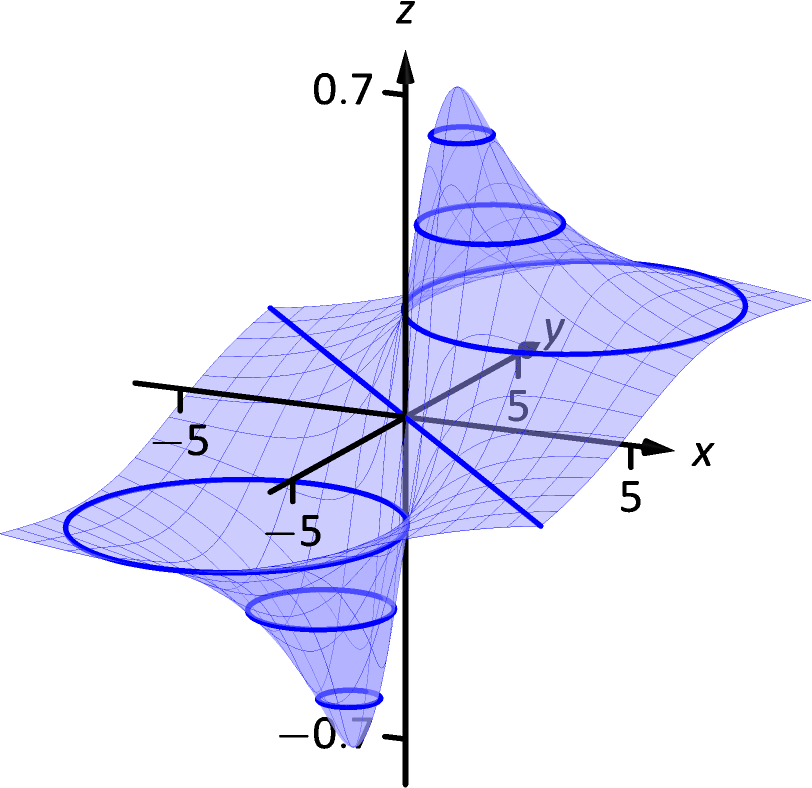


13 1 Introduction To Multivariable Functions Chapter 13 Functions Of Several Variables Part Calculus Iii



Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram



Level Curves



Calculus Iii Functions Of Several Variables



How Do You Sketch Level Curves Of Multivariable Functions Vector Calc Vector Calculus Calculus Math



Surface From Level Curves Of Unkown Levels In Matlab Stack Overflow
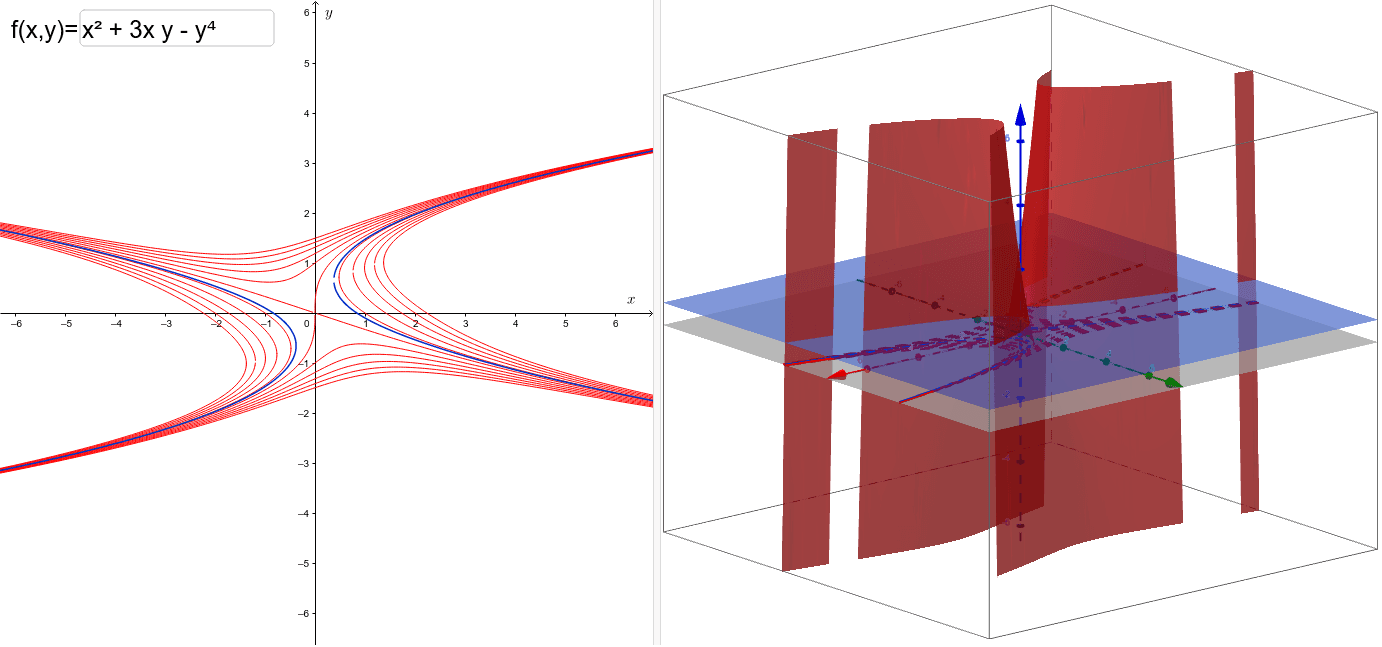


Level Curves Geogebra



Level Curves Of The Error Function Download Scientific Diagram



Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube



Gradients And Level Curves


Level Sets Ximera
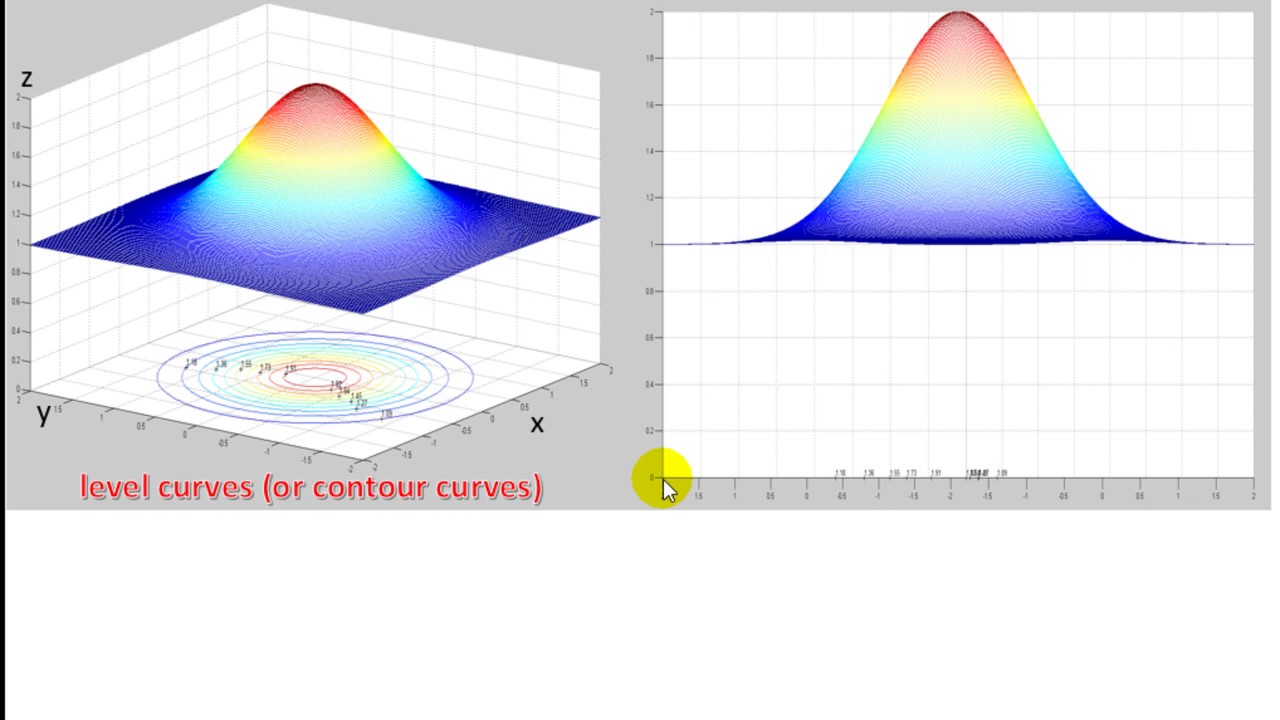


Level Curves Or Contour Curves Youtube



Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Math2111 Higher Several Variable Calculus Directional Derivative And Level Curves


Solved Use The Level Curves In The Figure To Predict The Chegg Com



A Intersection Of Level Curves Of I 1 And I 2 P A 1 A 2 Area Download Scientific Diagram



0 件のコメント:
コメントを投稿